2023年8月24日,国家自然科学基金委发布通告《关于2023年国家自然科学基金集中接收申请项目评审结果的通告》,amjs澳金沙门欢迎您国家自然科学基金集中接收申请项目立项7项,其中面上项目3项,青年项目4项。
国家自然科学基金聚焦基础与前沿,是培育我国源头创新能力、支持基础科学研究的主渠道,学院所获国家基金的数量与质量是评价学院科研实力与潜力的重要指标之一。
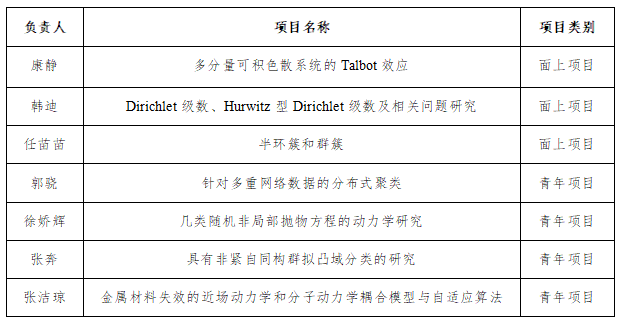
立项项目及负责人简介:
1.项目简介
Talbot效应是具有特定色散结构的色散系统在不连续初始值下的周期初边值问题的解所呈 现的一种特殊的二分现象,即相应的解在有理时刻呈现色散复苏现象,在无理时刻具有连续却 处处不可微的分形性态。Talbot效应既有典型物理背景,又有丰富数学内涵,近年来对它的研究得到了诸多数学家的关注。本项目拟在多分量框架下,聚焦Manakov和旋转Benjamin-Ono系统这两类典型的可积色散模型,研究其周期和拟周期初边值问题解的Talbot效应的数学理论。项目拟研究多分量可积色散系统的周期及拟周期演化的Talbot效应形成机理;探讨带有可积结构的非线性扰动机制;揭示多分量耦合、可积结构与色散结构相互制约,以及拟周期边界条件对相应解的Talbot效应影响因素;挖掘新的有理时刻色散复苏现象。
2.项目负责人简介

康静,教授,博士生导师。研究方向:非线性偏微分方程、数学物理与可积系统。主持国家自然科学基金面上项目3项、基金青年项目1项;主持陕西省杰出青年基金项目1项;参与国家自然科学基金重点项目1项;入选“陕西省高校首批青年杰出人才支持计划”。现任amjs澳金沙门欢迎您副院长,amjs澳金沙门欢迎您非线性科学研究中心副主任,“陕西省流体力学数学理论与计算重点实验室”副主任。
1.项目简介
Dirichlet L-函数、周期函数、Lerch 函数、Hurwitz L-函数等Dirichlet级数或Hurwitz型Dirichlet级数的均值估计及相关问题都是解析数论研究的中心问题,它们在素数分布以及数论中很多著名和式的算术性质研究方面等都有很重要的应用。本项目主要研究几类Dirichlet级数、Hurwitz 型Dirichlet级数的值分布与均值计算问题,并利用这些性质研究特征和、Dedekind型和的值分布性质,探讨这些和式在不同权下、不同数集上的值分布差异,以及Lehmer问题、整数逆与幂及其推广形式的分布问题。本项目力争获得一些改进或者突破性结果,丰富和完善相关理论。Dirichlet L-函数、周期函数、Lerch 函数、Hurwitz L-函数等Dirichlet级数或Hurwitz型Dirichlet级数的均值估计及相关问题都是解析数论研究的中心问题,它们在素数分布以及数论中很多著名和式的算术性质研究方面等都有很重要的应用。本项目主要研究几类Dirichlet级数、Hurwitz 型Dirichlet级数的值分布与均值计算问题,并利用这些性质研究特征和、Dedekind型和的值分布性质,探讨这些和式在不同权下、不同数集上的值分布差异,以及Lehmer问题、整数逆与幂及其推广形式的分布问题。本项目力争获得一些改进或者突破性结果,丰富和完善相关理论。
2.项目负责人简介

韩迪,副教授,硕士生导师,入选陕西省高校“青年杰出人才支持计划”。现任amjs澳金沙门欢迎您基础数学系主任,基础数学系党支部书记。美国《数学评论》评论员。研究方向为数论及其应用,发表论文20余篇,主持国家自然科学基金青年项目、陕西省自然科学基础研究计划项目、陕西省基础科学(数学、物理学)研究院科研计划项目各1项,并参与多项国家自然科学基金面上项目。获陕西省优秀博士学位论文奖、amjs澳金沙门欢迎您第十二届青年教师讲课比赛理工组一等奖、2019年amjs澳金沙门欢迎您教学奖、amjs澳金沙门欢迎您青年教师多媒体课件设计竞赛二等奖、2020年amjs澳金沙门欢迎您第二届课堂教学创新大赛一等奖;获得amjs澳金沙门欢迎您2021-2022教学年度优秀教师称号、第十三届全国大学生数学竞赛优秀指导教师称号。主讲课程为2019年-2022年新进教师岗前培训教学观摩课程;主持amjs澳金沙门欢迎您本科人才培养建设(课程思政类)项目“微积分”,参与陕西省教师教育改革与教师发展研究重点项目、amjs澳金沙门欢迎您教学研究与成果培育项目、amjs澳金沙门欢迎您精品在线开放课程项目“经济类《高等数学》”、amjs澳金沙门欢迎您高水平教材建设项目“《初等数论》教材建设”;指导学生参加全国大学生数学建模竞赛获全国一等奖1项、陕西赛区一等奖、二等奖10余项。
1.项目简介
簇是代数学中最基本、最重要的概念之一。簇理论中的Burnside问题、有限基问题和有限生成问题被诸多国内外数学家和计算机学家研究而远未得到完全解决,被公认是代数学中的困难问题,是簇理论研究的前沿、核心问题,与数论和理论计算机科学中的一些著名公开问题有着密切的联系。该项目聚焦半环簇和群簇,将利用泛代数的理论和方法,结合群论、半群代数理论、半环代数理论、超图理论和字的组合理论中的一些工具和技巧,独辟蹊径,系统深入地研究半环簇和群簇。该项目的研究目标是回答若干重要半环簇和群簇的Burnside问题,有限基问题和有限生成问题,从而完成一些半环簇和群簇的分类工作,且进一步深入揭示半环代数理论和群论之间的联系。该项目的实施将会进一步丰富和完善半环簇和群簇的内容和研究方法,为簇理论的研究提供新的视角和思路,培养一支优秀的簇理论研究队伍,开创我国在该研究领域的新局面。
2.项目负责人简介

任苗苗,陕西佳县人,副教授,硕士生导师。2015年6月在amjs澳金沙门欢迎您获得理学博士学位,毕业后留校任教至今。目前担任教育部学位中心的论文评审专家,美国数学评论杂志的特约评论员,Comm. Algebra, Semigroup Forum, Publ. Math. Debrecen, Asia-Euro. J. Math., 数学进展等期刊的匿名审稿人。研究方向为代数学,主要从事簇理论中一些核心问题的相关研究。在国内外刊物J. Algebra, Semigroup Forum, Algebra Universalis, Period. Math. Hungar., Acta Sci. Math. (Szeged), Linear and Multilinear Algebra等发表论文10余篇。主持完成了国家自然科学青年基金项目、陕西省自然科学基金青年项目、陕西省教育厅专项科研基金项目。获得了陕西省自然科学奖二等奖、陕西高等学校科学技术奖一等奖、陕西省数学会青年教师优秀论文一等奖、《纯粹数学与应用数学》楠竹奖励计划优秀论文奖三等奖。
1.项目简介
网络数据聚类是网络数据分析的基本任务之一,它旨在根据已知的网络结构,寻找节点所形成的类。随着科学技术的发展,从不同数据源可产生同一组对象的不同网络关系,从而形成多重网络数据。由于数据天然来自于不同数据源,再加上通信成本、数据隐私、数据所有权等方面的限制,多重网络中的每层网络往往分别存储于本地。在此背景下,项目拟围绕谱方法研究具有通信高效性、隐私保护性、数据异质性的分布式多重网络数据的聚类问题,建立一套完整的算法和统计理论分析框架,该框架的建立为存在数据共享约束、数据包含异质性等实际网络数据分析和应用场景提供理论基础和算法支撑。
2.项目负责人简介

郭骁,2019年获amjs澳金沙门欢迎您统计学博士学位,2018-2019年哥伦比亚大学统计系进行联合培养博士。现为amjs澳金沙门欢迎您统计系讲师。目前主要从事网络数据分析、数据隐私保护等研究。
1.项目简介
本项目关心三类含非局部算子的随机抛物方程的动力学问题,其背景来源于生物种群间的个体竞争,气候变迁和物理中的反常扩散现象。主要运用偏微分方程中的Galerkin方法、单调方法、紧嵌入定理和能量估计,结合随机动力系统中的停时理论、鞅理论和伊藤公式等工具,研究上述模型的适定性、解的收敛性和长时间行为。具体而言:(1)研究一类由布朗运动驱动的随机非局部分数抛物方程的适定性和随机吸引子的存在性,证明该模型的弱解收敛到对应的随机非局部经典抛物方程的弱解;(2)证明一类由布朗运动和Lévy噪声驱动的随机非局部分数抛物方程的适定性,弱均方吸引子和不变测度的存在性,遍历性和大偏差原理;(3)讨论不同噪声情形下一类含奇异核的随机非局部抛物方程的适定性和随机吸引子的存在性及其性质。本项目的研究结果有助于加深对自然界随机非局部现象的理解。此外,在研究过程中提出新的数学方法和技巧为同类问题的动力学研究提供新的思路。
2.项目负责人简介

徐娇辉,amjs澳金沙门欢迎您副教授。本硕就读于兰州大学,博士就读于西安交通大学,并于2021年取得博士学位。2019.10-2021.04受国家留学基金委资助访问西班牙塞维利亚大学T. Caraballo教授,2021.07-2022.12跟随T. Caraballo教授在塞维利亚大学继续博士后研究。主要研究方向是随机动力系统,目前已在SIAM J. Math. Anal, J. Differential Equations, J. Dynam. Differential Equations 等数学杂志上发表论文十余篇。
1.项目简介
拟凸域的分类是多复变中的一个重要课题。域上的全纯自同构群是一个重要的全纯不变量,自同构群的结构在某些方面反应了域的几何结构。特别是在自同构群非紧的情况下,可以利用边界轨道聚积点的type给出拟凸域的分类。本项目的研究可为拟凸域的分类问题提供新方法、新思路,同时本项目的研究思路和方法对拟凸域上的度量等价性问题也有促进作用。
2.项目负责人简介

张奔,博士研究生,讲师,2017年入职amjs澳金沙门欢迎您,主要研究方向为多复变函数论与复几何,具体研究拟凸域的分类,不变度量的等价性。近年来发表论文5篇。
1.项目简介
金属材料在不同载荷作用下微观晶体结构的变形、损伤及失效行为直接影响其使用性能和服役寿命。从微观尺度出发,发展数学模型及算法研究其跨原子-连续尺度的损伤及失效机制是数学与力学、材料科学等学科交叉的前沿研究课题。本项目将针对金属失效中的关键科学问题,结合分子动力学与新兴的近场动力学模型,开展多尺度建模及自适应耦合算法研究。研究内容包括:基于分子动力学中原子相互作用势能函数,建立参数传递的串行多尺度模型,实现近场动力学本构方程及损伤失效准则的精确校准;建立含损伤失效准则的近场动力学和分子动力学并行耦合模型,提供损伤及失效的精细化数学建模;发展该模型的自适应耦合的快速算法,实现对变形-跨尺度损伤-失效过程的快速数值模拟。本项目的研究将为金属材料跨尺度的变形、损伤及失效行为提供高效率、高精度的模拟方案,推进对失效机理的认知,研究成果将从理论模型和数值算法方面为金属材料的设计和制造提供理论和技术支撑。
2.项目负责人简介

张洁琼,女,中共党员,2020年7月毕业于西北工业大学并获得理学博士学位,于同年9月份入职amjs澳金沙门欢迎您。主要的研究方向包括:非局部模型耦合及算法,材料损伤及断裂的分子动力学和近场动力学理论及数据驱动的机器学习模型等。目前已经在计算数学及数学与其他方向的交叉方向的重要期刊Computer Methods in Applied Mechanics and Engineering, Computational Mechanics,Engineering with Computers, Theoretical and Applied Fracture Mechanics, Communications in Computational Physics等发表相关学术论文6 篇。现主持国家自然科学基金1项,陕西省教育厅专项科研基金1项。
amjs澳金沙门欢迎您以“基础学科试点改革”为契机,紧盯国家战略和学科前沿,积极凝练学科方向,组建新兴科研团队,狠抓科研项目与成果孵化,并初具特色和成效。此次国家自然科学基金立项结果为所在科研团队和负责人长期坚守学科特色、潜心研究的阶段性成果。
特向立项的老师及团队祝贺!向全院师生报喜!